Le rôle du contrôle de gestion dans le calcul et l’analyse des écarts sur coûts consiste à comparer les coûts constatés aux coûts standards pour mettre en évidence les écarts significatifs, à rechercher les causes de ces écarts, à mettre en œuvre des actions correctives afin d’apprécier et d’améliorer les performances internes de l’entreprise.
Le principe de calcul des écarts
Un écart est défini comme la différence entre une donnée de référence (coût préétabli…) et une donnée constatée (coût réel…). Chaque écart est évalué en valeur monétaire et calculé, par convention, de la manière suivante :
Écart = Coût constaté- Coût standard
L’écart peut être positif ou négatif :
Le modèle d’analyse des écarts sur coûts
Seuls les écarts significatifs, c’est-à-dire ceux qui dépassent le seuil de tolérance fixé par l’entreprise, doivent faire l’objet d’une analyse. Une étude pertinente de la cause des écarts est menée en décomposant chaque écart en autant de facteurs qui le composent.
L’architecture suivante est le plus souvent retenue :
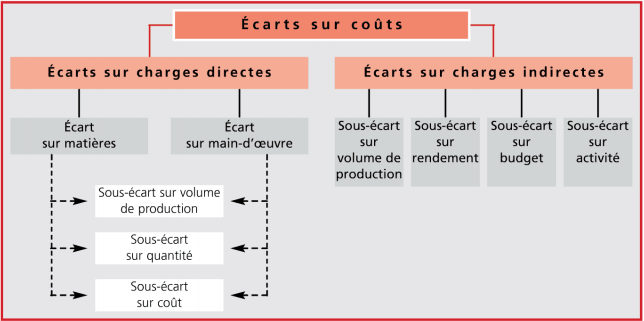
Les écarts sur charges directes
On distingue trois niveaux d’analyse pour chaque composante du coût direct du produit :
- écart total
- écart global
- sous-écarts
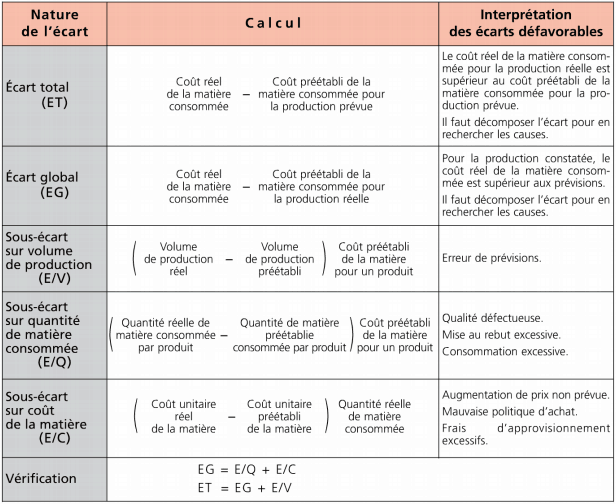
Les écarts sur matières
Un tableau récapitulatif des écarts sur matières est présenté ci-dessous :
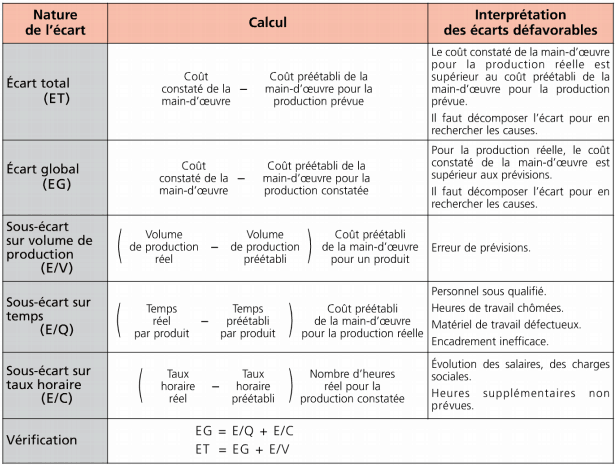
Les écarts sur main-d’œuvre
Un tableau récapitulatif des écarts sur main-d’œuvre est présenté ci-dessous :
Les représentations graphiques
On distingue deux représentations graphiques des écarts :
- sous d’aires
- sous forme vectorielle
Représentation graphique sous forme d’aires :
Les quantités réelles (Qr) et préétablies (Qp) sont portées en abscisse, les coûts réels (Cr) et préétablis (Cp) en ordonnée. Les écarts sont représentés par des aires de rectangles. Par exemple, dans le cas d’un écart sur coût et d’un écart sur quantité positifs, donc défavorables, la représentation graphique est la suivante :
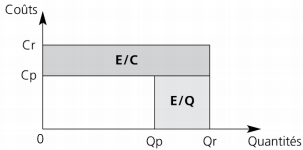
Les parties grisées représentent l’écart global.
E/C > 0
E/Q > 0
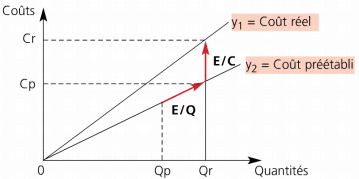
Représentation graphique sous forme vectorielle:
Le coût constaté et le coût préétabli sont représentés par des droites de la forme : y = ax
a = Coût unitaire
x = Quantité
L’écart sur quantité est représenté sous la forme d’un vecteur, sur la droite du coût préétabli.
L’écart sur coût est représenté sous la forme d’un vecteur qui joint les deux droites au niveau de la quantité réelle. Par exemple, dans le cas d’un écart sur coût et d’un écart sur quantité positifs, donc défavorables, la représentation graphique est la suivante :
Exemple :
Une société fabrique un produit A à l’aide d’une matière première M La production prévue est de 2 000 produits A, la production réelle est de 1 900 produits A. Fiche de coût standard pour un produit :
4 kilogrammes de matière M a 20 € le kg
2 heures de main-d’œuvre à 90 € l’heure
Coût réel pour un produit :
4,3 kilogrammes de matière M à 19,50 € le kg
1 heure 45 minutes de main-d’œuvre à 95 € l’heure
Écart sur matière
– Écart total :
(4,3 x 19,5 x 1 900) – (4 x 2 0 x 2 000) = – 685 € => écart favorable
La production de 1 900 produits A a coûté moins cher en matière première que la production prévue de 2 000 produits A
– Écart global :
(4,3 x 19,5 x 1 900) – (4 x 20 x 1 900) = 7 315 € => écart défavorable
La production de 1 900 produits A a coûté plus cher en matière première que prévu.
-Sous-écart sur volume de production :
(1 900- 2 000) 4 x 20 = – 8 000 € => écart défavorable
Bien que l’écart soit négatif, il ne doit pas être interprété comme favorable car produire moins que prévu n’est pas bénéfique pour l’entreprise.
-Sous-écart sur quantité de matière M consommée :
(4,3 – 4) 20 x 1 900 = 11 400 € => écart défavorable
Il a fallu consommer 300 grammes de matière première M en plus par produit, ce qui entraîne un surcoût de 11 400 € pour la fabrication de 1 900 produits A.
– Sous-écart sur coût de la matière M :
(19,50 – 20) 4,3 x 1 900 =- 4 085 € => écart favorable
Le kilogramme de matière première a coûté moins cher que prévu, ce qui entraîne une économie de 4 085 € pour la fabrication de 1 900 produits A
– Vérification : EG = 11 400 + (- 4 085) = 7 3 1 5 ; ET = 7 3 1 5 +(- 8 000) =- 685 €
Écart sur main-d’œuvre
– Écart total :
(1,75 x 95 x 1 900) – (2 x 90 x 2 000) = – 44 125 €=> écart favorable
La production de 1 900 produits A a coûté moins cher en main-d’œuvre que la production de 2 000 produits A prévue.
– Écart global :
(1,75 x 95 x 1 900) – (2 x 90 x 1 900) =- 26 125 € => écart favorable La production de 1 900 produits A a coûté moins cher en main-d’œuvre que prévu.
-Sous-écart sur volume de production :
(1 900 – 2 000) 90 x 2 =- 18 000 € => écart défavorable
Bien que l’écart soit négatif, il ne doit pas être interprété comme favorable car produire moins que prévu n’est pas bénéfique pour l’entreprise.
– Sous-écart sur temps :
(1,75 – 2) 90 x 1 900 =- 42 750 € => écart favorable
Il a fallu moins de temps que prévu pour fabriquer un produit A, ce qui entraîne une économie de coût de main-d’œuvre de 42 750 €.
-Sous-écart sur taux horaire :
(95 – 90) 1,75 x 1 900 = 16 625 € => écart défavorable L’heure de main-d’œuvre a été rémunérée 5 de plus que prévu ; on constate donc un surcoût de 16 625 € pour les 1 900 produits A- Vérification : EG =-42 750+ 16 625 =- 26 125 € ; ET=- 26 125 +(-18 000)=-44 125 €
Les écarts sur charges indirectes
On distingue trois niveaux d’analyse pour chaque centre d’analyse :
- écart total
- écart global
- sous-écarts
L’évaluation de l’écart global nécessite d’adapter les coûts standards à la production réelle ;
pour cela, il faut déterminer :
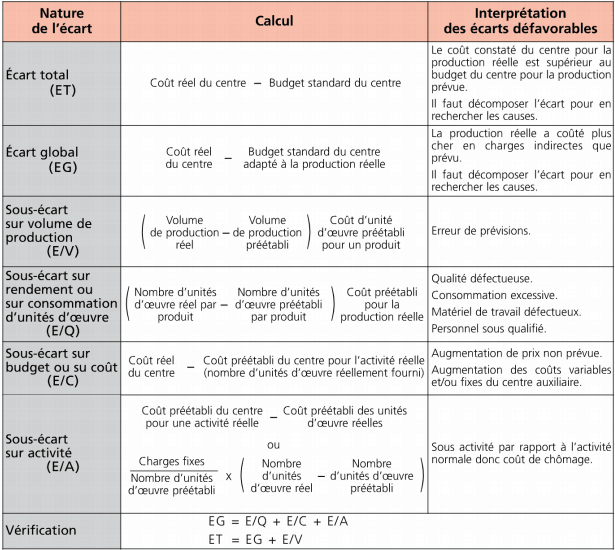
Un tableau récapitulatif des écarts sur charges indirectes est présenté ci-dessous :
Les représentations graphiques des écarts sur charges indirectes sont de mêmes formes que celles relatives aux charges directes.
Exemple:
Une entreprise fabrique un produit T dans un centre atelier.
Production prévue 1 000 produits T ; production réelle 1 200 T.
Budget du centre atelier :
2 heures machine par produit
40 000 de coûts fixes
70 de charges variables pour une heure machine
Coût préétabli de l’unité d’œuvre : ((70 x 2 000) + 40 000):2 000 = 90 €
Données réelles du centre atelier :
Coût réel du centre : 240 000 €
Nombre d’unités d’œuvre : 2 100 heures machine
Calcul et analyse des écarts
– Écart total :
240 000 – (90 x 2 000) = 60 000 => écart défavorable
La production de 1 200 produits T a coûté plus cher en charges indirectes que la production de 1 000 produits T prévue.
– Écart global :
240 000 – (90 x 2 x 1 200) = 24 000 => écart défavorable
La production de 1 200 produits T a coûté plus cher en charges indirectes que prévu.
-Écart sur volume de production :
(1 200 – 1 000) 90 x 2 = 36 000 => écart favorable
Bien que l’écart soit positif, il ne doit pas être interprété comme défavorable car produire plus que prévu est le plus souvent bénéfique pour l’entreprise.
-Sous-écart rendement :
((2100/1200)-2 ) 90 x 1 200 = – 27 000 => écart favorable
L’entreprise a consommé moins d’heures machine par produit que prévu, ce qui entraîne une économie de coût de 27 000 pour 1 200 produits.
-Sous-écart sur budget :
240 000 – [40 000 + (70 x 2 100)] = 53 000 => écart défavorable
Les charges réelles indirectes de l’atelier sont supérieures de 53 000 par rapport au budget adapté à l’activité réelle.
-Sous-écart sur activité :
[40 000 + (70 x 2 100)] – (90 x 2 100) = – 2 000 => écart favorable
L’entreprise constate un bonus de suractivité car le niveau d’activité réel est supérieur au niveau
d’activité préétabli.
-Vérification :
EG = – 27 000 + 53 000 + (- 2 000) = 24 000
ET = 24 000 + 36 000 = 60 000


Mamoudou
C’est bien j’aime bien votre démonstration