On met ci-après 26 exercices corrigés de statistique descriptive à une variable. On a divisé ces exercices en 3 parties . On commence avec le premier exercice : Le tableau ci-dessous donne la répartition des salaires mensuels, en euros, des employés d’une entreprise :
On vous demande de :
- Représenter cette série par un diagramme circulaire.
- Calculer le salaire moyen dans cette entreprise. Que penser d’un tel résultat ?
- Dans cette entreprise, combien d’employés gagnent au plus 1050 euros ?
Dresser le polygone des effectifs cumulés croissants et lire une valeur approchée de la médiane et de Q1 et Q3 - Calculer de manière précise la médiane et les quartiles Q1 et Q3
- Calculer l’écart type de cette série statistique.
- Dans cette série statistiques se rajoute une sixième catégorie d’employés dont les salaires appartiennent à la classe [1300 ;1500[. Quel est l’effectif de cette classe sachant que le salaire moyen au sein de cette entreprise est alors de 1200.
Correction du premier exercice de statistiques :

Télécharger “exercice corrigé de statistiques à une variable” Téléchargé 6190 fois – 291,66 Ko
Exercice 2 de statistiques à une variable
A. Les 35 élèves d’une classe ont composé et le tableau ci-dessous donne la répartition des diverses notes.
Recopier et compléter ce tableau en calculant les fréquences à ![]() près, et les effectifs cumulés croissants et décroissants.
près, et les effectifs cumulés croissants et décroissants.
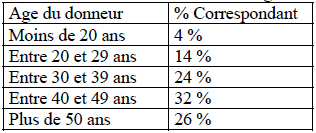
B. Un établissement de transfusion sanguine a dressé le bilan de sa collecte de sang pendant un an.
Représenter cette série statistique par un diagramme circulaire.
Solution de l’exercice 2 de statistiques à une variable :
A.
B. On dresse un tableau de proportionnalité entre chaque fréquence et l’angle du secteur angulaire correspondant.
Exercice 3 de statistique à une variable
A. Un industriel a commandé à un sous-traitant un lot de 40 pièces dont le diamètre doit mesurer 80 mm et il est convenu que le lot ne sera accepté que si les deux conditions suivantes sont simultanément réalisées :
Première condition : l’écart entre 80 mm et la moyenne ![]() du lot est inférieur à 0,05 mm.
du lot est inférieur à 0,05 mm.
Deuxième condition : Au moins 60 % des pièces du lot ont un diamètre d tel que 80−0,05≤d≤80+0,05 (1)
Les mesures faites sur le lot sont les suivantes :
1) Calculer la moyenne x des mesures faites
2) Quel est le pourcentage de pièces dont le diamètre d vérifie la double inégalité (1) ?
3) Le lot est-il accepté ou refusé par l’industriel ? Justifier la réponse
B. Un élève a obtenu les notes suivantes : 4;6;3;9;10;8;12;10;19;12;20;12;18 . Calculer sa moyenne
C.
1) Calculer
2) Écrire en utilisant la notation Σ: 3+5+7+9+…15+17
Solution de l’exercice 3 de statistiques à une variable :
A.
1) La moyenne ![]() des mesures faites vaut :
des mesures faites vaut :
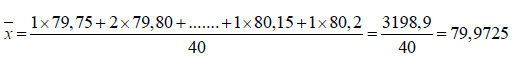 2) Le nombre de pièces dont le diamètre d vérifie la double inégalité (1) est égal à 6+14+5=25, soit un pourcentage égal à 25/40 *100 = 62,5%
2) Le nombre de pièces dont le diamètre d vérifie la double inégalité (1) est égal à 6+14+5=25, soit un pourcentage égal à 25/40 *100 = 62,5%
3) L’écart entre la moyenne x et 80 mm étant égal à 80−79,9725=0,0275<0,05, et plus de 60 % des pièces ayant un diamètre d vérifiant la double inégalité (1), le lot sera accepté.
B.
La moyenne de l’élève est égale à :
C.
1) 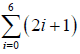 = 2×0+1+2×1+1+2×2+1+2×3+1+2×4+1+2×5+1+2×6+1=49
= 2×0+1+2×1+1+2×2+1+2×3+1+2×4+1+2×5+1+2×6+1=49
Exercice 4 de statistiques à une variable
Un relevé des durées des communications téléphoniques effectués dans un central téléphonique a fourni les informations consignées dans le tableau suivant (l’unité de durée est la minute).
Travail à faire:
1) Calculer la durée moyenne d’un appel
2) On regroupe les classes par deux, ce qui revient à considérer les classes [0;4[, [4,8[ et [8;12[. Calculer la durée moyenne d’un appel pour cette nouvelle série
3) Quelle conclusion pouvez-vous formuler ?
Solution de l’exercice 4 de statistiques à une variable:
1) Pour calculer la moyenne de cette série statistique, on prend en compte le milieu des classes, à savoir :
La durée moyenne d’un appel vaut donc :
Soit 5 minutes et 0,88×60=52,8 secondes.
La durée moyenne d’un appel vaut donc 5 minutes, 52 secondes et 8 dixièmes.
2) La nouvelle série statistique est donc:
Pour calculer la moyenne de cette série statistique, on prend en compte le milieu des classes, à savoir :
La durée moyenne d’un appel calculée à partir de cette série vaut donc :
3) Selon la manière de regrouper les communications téléphoniques (donc seulement la présentation de la série statistique !), les résultats peuvent être différents.
Exercice de statistique sur la représentation graphique avec interprétation
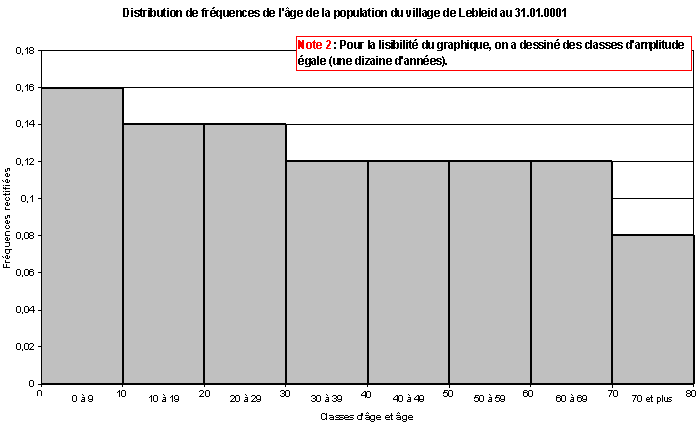
Dans cet exercice On vous demande : premièrement de faire Une représentation graphique la plus précise possible de la distribution de fréquences de l’âge des personnes résidant dans le village de Lebleid au 31.12 An 1. Deuxièmement de faire Une interprétation de ce graphique.
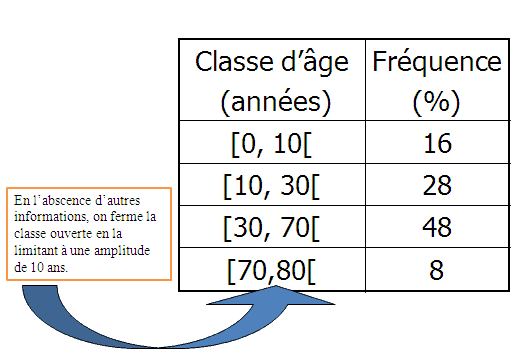
On trouve dans l’annuaire statistique du pays voisin, le Chéseu, le tableau suivant :

Principes de solution:
- On tient compte de toute l’information, pas seulement du tableau.
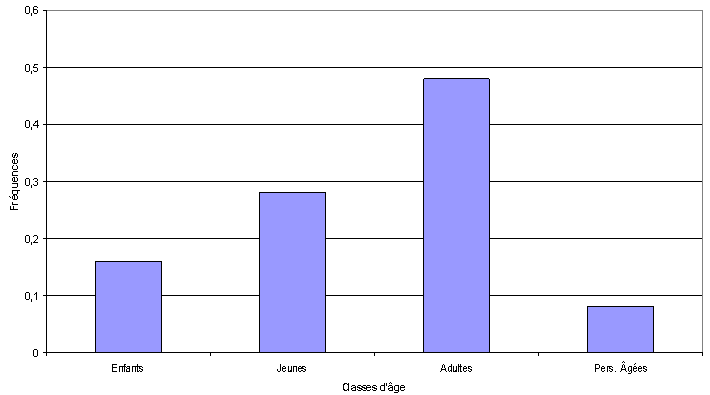
- Si on tenait compte uniquement du tableau, la variable serait considérée comme une variable qualitative mesurée sur une échelle ordinale et la représentation la plus appropriée aurait été celle du graphique 1.
- Le graphique circulaire n’est pas approprié puisque les classes d’âge sont mesurées sur une échelle au minimum ordinale.
- En tenant compte de la note méthodologique, on remarque que nous avons affaire à une variable quantitative continue, mesurée sur une échelle proportionnelle, regroupée en classes d’inégale amplitude.
Traitement de la variable âge:
On peut réaliser le tableau suivant servant de base au graphique 2 :
Graphique 1
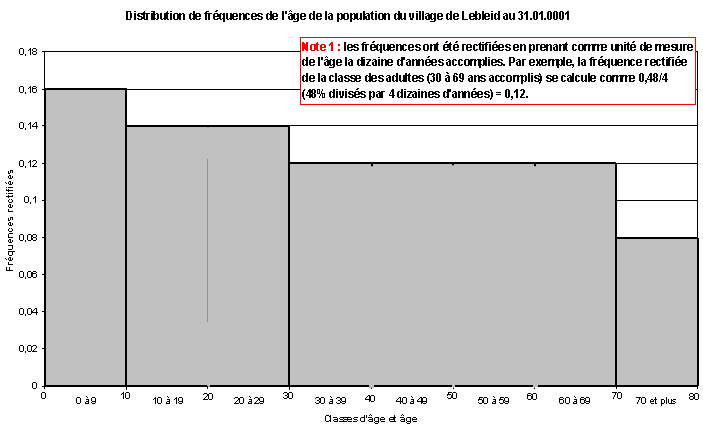
distribution de fréquences de l’age de la population du village lebleid au 31-01-01
Conclusion:
- La fréquence rectifiée diminue avec l’âge.
- Contrairement à ce que qu’aurait pu laisser croire une première lecture rapide du tableau de l’énoncé ou le graphique 1, le graphique 2 indique que la population du village est jeune. (La base de la pyramide des âges est large).
Exercice 5 : moyenne, médiane, quartiles
A: Dans un sous-groupe de 40 personnes la taille moyenne est de 170 cm. Dans un deuxième sous-groupe de 10 personnes la taille moyenne est de 180 cm. Dans un troisième sous-groupe de 50 personnes la taille moyenne est de 175 cm.
- Déterminer la taille moyenne du groupe constitué par les trois sous-groupes précédents.
- Quelle serait la taille moyenne si les trois sous-groupes étaient constitués du même nombre de personnes ?
B: La température est relevée chaque heure pendant 4 jours dans une forêt. Les 97 résultats obtenus ont été triés et sont rassemblés dans le tableau suivant :
- Déterminer la médiane M, les quartiles Q1 et Q3 de celle série statistique.
- On appelle premier décile (noté D1) la plus petite valeur de la température telle qu’au moins 10% des valeurs sont inférieures ou égales à D1. On appelle neuvième décile (noté D9) la plus petite valeur telle qu’au moins 90% des valeurs lui sont inférieures ou égales.
Justifier que D1 = 15 et calculer D9.
Correction:
A:
1) Pour calculer la moyenne du groupe constitué par ces trois sous groupes, il faut tenir compte des effectifs de chacun de ces sous-groupes.
La moyenne du groupe des 40+10+50=100 personnes vaut donc:
2) Si les trois sous-groupes étaient constitués du même nombre de personnes, il suffirait de concéder la moyenne arithmétique des trois valeurs 170,180 et 175. En effet, si on note x l’effectif commun des trois sous-groupes, alors la moyenne générale vaudra:
B:
1) Puisque le nombre d’observations est impair (97=2×48+1), la médiane M sera égale à la 49ème mesure de température, c’est-à-dire, en observant le tableau, à 16,5° (la 49ème observation fait partie des 15 mesures égales à 16,5°)
Le quartile Q est la plus petite valeur du caractère pour laquelle 25 % des valeurs de la série statistique lui sont inférieures ou égales. Puisque 25% de l’effectif total représentent 97×25/100= 24,25 , le quartile Q1 correspondra à la 25ème mesure, c’est-à-dire 16°.
De même, le quartile Q3 est la plus petite valeur du caractère pour laquelle 75 % des valeurs de la série statistique lui sont inférieures ou égales. Puisque 75% de l’effectif total représentent 97×75/100=72,75, le quartile Q3correspondra à la 73ème mesure, c’est-à-dire 18°.
2) Le décile D1 est la plus petite valeur du caractère pour laquelle 10 % des valeurs de la série statistique lui sont inférieures ou égales. Puisque 10% de l’effectif total représentent 97×10/100=9,7 , le décile D1 correspondra à la 10ème mesure, c’est-à-dire 15°
De même, le décile D9 est la plus petite valeur du caractère pour laquelle 90 % des valeurs de la série statistique lui sont inférieures ou égales. Puisque 90% de l’effectif total représentent 97×90/100=87,3 , le décile D9 correspondra à la 88ème mesure, c’est-à-dire 19°
3 Exercices corrigés de statistique descriptive
On met à votre disposition des exercices de statistiques descriptive, ces exercices portent sur le vocabulaire de base de cette matière : La population, unités statistiques, caractère qualitatif et caractère quantitatif,….etc

Télécharger “Exercices corrigés : Statistiques descriptive” Téléchargé 1551 fois – 344,22 Ko
11 exercices corrigés de statistique
On met ci-dessous une série de 11 exercices corrigés de statistique descriptive en PDF. ces exercices concernent le calcul de la moyenne, la médiane, l’écart-type …
Télécharger “11 exercices corrigés de statistique” Téléchargé 898 fois – 1,18 Mo
7 Exercices de statistique descriptive univariée et bivariée
Ci-dessous on met à votre disposition 7 exercices de statistique univariée. Les 4 premiers exercices concernent la statistique univariée, les trois derniers portent sur la statistique descriptive bivariée.
Télécharger “7 Exercices de statistique descriptive” Téléchargé 561 fois – 1,11 Mo
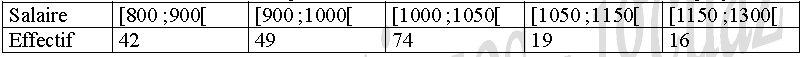
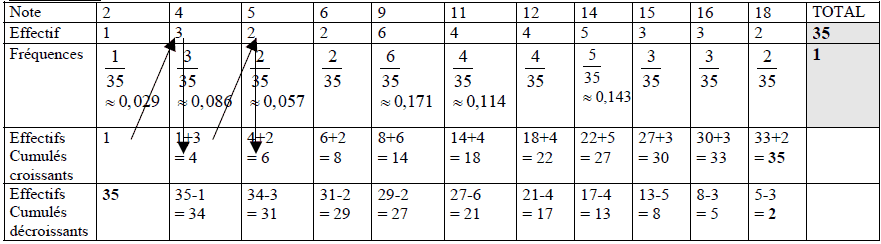


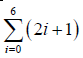
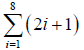

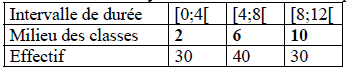
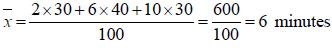

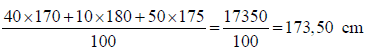
yessoh
très bon site pour les étudiants et enseignants en vue de leur performance en math.
Jimmy Georges Gilbert
Très intéressant bro. Je tires directement quelques questions.
Mahaman Siradji Abass
Très rentable merci pour votre aide