On met ci-dessous un exercice corrigé de statistique sur les Moyennes, les quartiles et le diagramme. Les moyennes, les quartiles et les diagrammes sont tous des concepts importants en statistiques pour résumer et visualiser des données. Voici une brève explication de chacun d’entre eux :
Exercice de statistique sur la Moyenne, les quartiles et les diagrammes

1. Définition de la Moyenne :
La moyenne est une mesure de tendance centrale qui représente la valeur moyenne d’un ensemble de données. Pour la calculer, vous additionnez toutes les valeurs de données et divisez le total par le nombre de données. La formule de la moyenne est la suivante :
Moyenne = (Somme des données) / (Nombre de données)
La moyenne est sensible aux valeurs extrêmes, ce qui signifie qu’elle peut être influencée par les valeurs aberrantes.
2. Définition des Quartiles:
Les quartiles sont des valeurs qui divisent un ensemble de données triées en quatre parties égales. Il y a trois quartiles principaux :
– Premier quartile (Q1) : Divise les 25 % inférieurs des données.
– Deuxième quartile (Q2) : Équivaut à la médiane, divisant les données en deux moitiés égales.
– Troisième quartile (Q3) : Divise les 25 % supérieurs des données.
Les quartiles sont utilisés pour analyser la dispersion des données et identifier les valeurs extrêmes.
3. Diagrammes (ou graphiques) statistiques :
Les diagrammes statistiques sont des représentations graphiques des données qui aident à visualiser et à comprendre les tendances et les caractéristiques d’un ensemble de données. Il existe de nombreux types de diagrammes, notamment :
- Diagramme en barres : Utilisé pour représenter des catégories discrètes.
- Diagramme en secteurs : Idéal pour montrer la répartition des catégories dans un ensemble de données.
- Diagramme en boîte (ou boîte à moustaches) : Utilisé pour afficher la distribution des données, y compris les quartiles et les valeurs aberrantes.
- Diagramme en nuage de points : Utile pour montrer la relation entre deux variables continues.
- Histogramme : Affiche la distribution de données continues en créant des intervalles (bin) de données.
- Diagramme en ligne : Utilisé pour représenter des données sur une période.
Exercice corrigé sur les Moyenne, quartiles et diagramme
Le tableau ci-dessous donne la répartition des salaires mensuels, en euros, des employés d’une entreprise :
 Calculer le salaire moyen dans cette entreprise. Que penser d’un tel résultat ?
Calculer le salaire moyen dans cette entreprise. Que penser d’un tel résultat ?- Dans cette entreprise, combien d’employés gagnent au plus 1050 euros ?
Dresser le polygone des effectifs cumulés croissants et lire une valeur approchée de la médiane et de Q1 et Q3 - Calculer de manière précise la médiane et les quartiles Q1 et Q3
- Construire le diagramme en boîte de la série statistique
Solution:
- Pour calculer le salaire moyen de l’entreprise, il faut considérer le milieu de chaque classe :
 Le salaire moyen dans cette entreprise est donc de 993 €. Il n’est pas forcément très représentatif de cette entreprise, car plus de la moitié des employés y gagnent plus de 1000 euros !
Le salaire moyen dans cette entreprise est donc de 993 €. Il n’est pas forcément très représentatif de cette entreprise, car plus de la moitié des employés y gagnent plus de 1000 euros !
2. Pour répondre à cette question, il faut dresser le tableau des effectifs cumulés croissants :
Ainsi, 165 employés gagnent au plus 1050 euros, au sein de cette entreprise
A partir de ce tableau, on dresse le polygone des effectifs cumulés croissants.
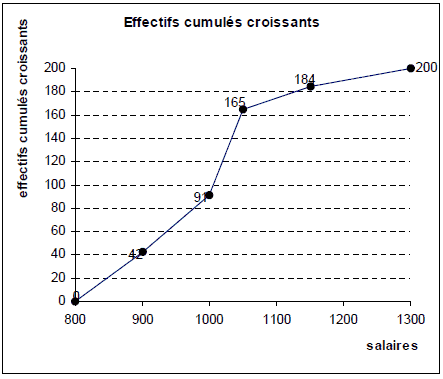 A partir de ce polygone, on cherche le salaire médian, c’est-à-dire celui qui va partager la série statistique en deux parties d’égale amplitude. Il s’agit donc du salaire correspondant à un effectif cumulé de 100 salariés (moitié de l’effectif).
A partir de ce polygone, on cherche le salaire médian, c’est-à-dire celui qui va partager la série statistique en deux parties d’égale amplitude. Il s’agit donc du salaire correspondant à un effectif cumulé de 100 salariés (moitié de l’effectif).
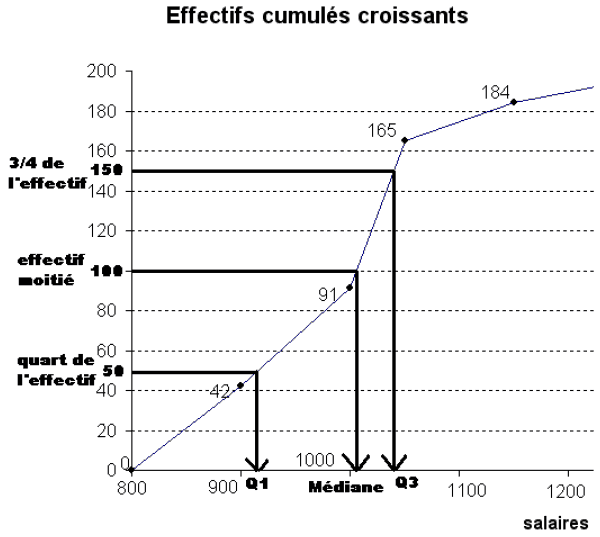
On se place ainsi que l’axe des ordonnées à l’effectif cumulé 100, et on lit l’antécédent de 100. Ce sera la médiane. On procède de même avec les quartiles Q1 et Q3, qui correspondent respectivement à un effectif cumulé de 1/4 x200 = 50 et de 3/4 x 200 = 150 On lit graphiquement que Médiane ≈ 1010 , Q1≈915 et Q3≈1050
3) Calcul précis de la moyenne et des quartiles Q1 et Q3
Pour calculer la médiane, on va réaliser une interpolation linéaire entre les points A(1000 ;91) et B(1050 ;165)
L’équation de la droite (AB) est de la forme :
Pour trouver la valeur de p , on utilise les coordonnées de A (ouB !) :
![]() L’équation de (AB) est donc: 1,48x- 1389 . On trouve la médiane en calculant l’antécédent de la moitié de l’effectif (c’est à dire 200/2=100) par la fonction affine :
L’équation de (AB) est donc: 1,48x- 1389 . On trouve la médiane en calculant l’antécédent de la moitié de l’effectif (c’est à dire 200/2=100) par la fonction affine :
![]() c’est-à-dire en résolvant l’équation 1,48x−1389=100⇔x= 1489/1.48 ≈1006,08
c’est-à-dire en résolvant l’équation 1,48x−1389=100⇔x= 1489/1.48 ≈1006,08
Ainsi Me≈1006
Puisque le quartile Q3 semble lui aussi appartenir à l’intervalle [1000;1050[, on utilise la même droite, et on résout l’équation 1,48x−1389=150 ⇔ 1539/1.48
≈ 1039,86
Ainsi Q3≈1040
De la même manière, pour déterminer le quartiles Q1, on doit déterminer l’équation de la droite reliant les points (900 ;42) et (1000 ;91). Cette droite a pour équation v=0,49x−399, et la résolution de l’équation 0,49x-399=50 ⇔
x= 449/0.49 ≈ 916,33 fournit Q1≈916
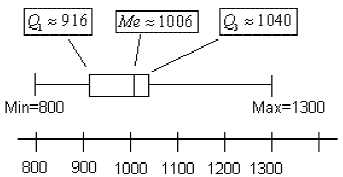
4.Le diagramme en boîte de la série est donné par :
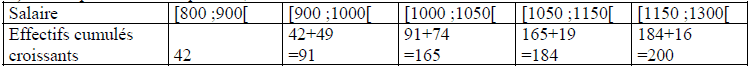
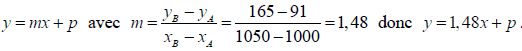
Laisser un commentaire