A:Après correction des copies, la moyenne à l’épreuve de mathématiques au baccalauréat est de 8,4.
1) Si le ministre de l’Education Nationale décide d’augmenter la note de chaque copie de 1,6 point, quelle sera la nouvelle moyenne nationale ?
2) Si le ministre de l’Education Nationale décide d’augmenter la note de chaque copie de 10%, quelle sera la nouvelle moyenne nationale ?
B: On considère les deux séries statistiques définies par les tableaux T1 et T2 ci-dessous :
 1) Calculer la moyenne de la série statistique correspondant à T1
1) Calculer la moyenne de la série statistique correspondant à T1
Déduire de ce résultat la moyenne de la série correspondant à T2
2) Lors de l’étude sur la résistance d’un type de fil, on a réalisé cent expériences de rupture et on a noté à chaque fois la charge limite provoquant la rupture. Les résultats sont consigné dans le tableau suivant:
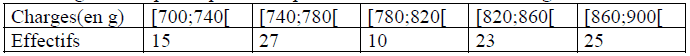 Utilisez un des deux résultats précédents pour obtenir rapidement la moyenne de la charge de rupture.
Utilisez un des deux résultats précédents pour obtenir rapidement la moyenne de la charge de rupture.
Solution:
A:
Après correction des copies, la moyenne à l’épreuve de mathématiques au baccalauréat est x=8,4.
1) Si les valeurs de la série statistique sont toutes augmentées d’une même valeur, sans modifier les effectifs, alors la moyenne subit la même transformation. La nouvelle moyenne de l’épreuve sera donc égale à 8,4+1,6=10
2) Augmenter une quantité de 10% revient à la multiplier par 1,1
Si les valeurs de la série statistique sont toutes multipliées par une même valeur, sans modifier les effectifs, alors la moyenne subit la même transformation. La nouvelle moyenne de l’épreuve sera donc égale à 1,1×8,4=9,24
B:
1) La moyenne de la série statistique correspondant à T1 est égale à :
On remarque que les valeurs de la série statistique du tableau T2 sont égales à celles du tableau T1 augmentées de 100, les effectifs correspondants étant identiques.
La moyenne de la série correspondant à T2 est donc égale à celle de de la série correspondant à T1 augmentée de 100, donc
X2=X1+100=106,4
2) Pour calculer la moyenne de la charge de rupture, il faut considérer les milieux de chaque classe, donc la série statistique :

On reconnaît les valeurs de la série statistique correspondant à T2 augmentées de 700.
La moyenne de la charge de rupture vaut donc X2+700=106,4+700=806,4 grammes
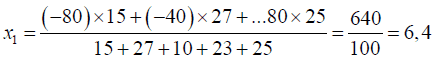
Laisser un commentaire