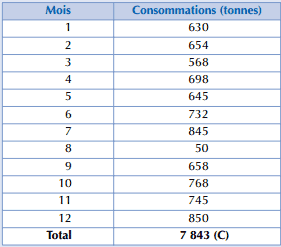
Avant de faire l’exercice merci de consulter le cours sur le lien suivant « Comment Optimiser le budget – achats ?« . Une entreprise a établi son budget prévisionnel de consommation d’une matière première stratégique dont les approvisionnements sont parfois sujets à des aléas. En conséquence, le stock minimum est fixé à deux mois de consommation moyenne.
Exercice sur la gestion des approvisionnements:
Les différents paramètres afférents aux approvisionnements sont les suivants :
- le coût d’achat d’une tonne est de 7 200 €(p) ;
- le coût fixe d’une commande est de 45 000 €(f) ;
- le coût de stockage représente 15 % de la valeur du stock (t) ;
- le stock initial est de 2545 tonnes ;
- le délai d’approvisionnement est de 3 semaines ;
- le stock de sécurité est fixé à deux mois au minimum. À la fin de l’année, il doit représenter au moins 2500 tonnes;
- les commandes sont passées en début de mois par cent tonnes et les commandes arrivent à la fin du mois.
L’application directe de la formule de Wilson donne la cadence optimale d’approvisionnement.
Quantité optimale commandée : Q* = [(2 . C . f) / (p . t)]½
Cadence d’approvisionnement optimale : N* = C / Q*
Soit :
N* = [C . (p . t)½] / (2 . C . f)½ = [(C . p . t) / (2 . f)]½
N* = [(7843 . 7200 . 0,15) / (2 . 45000)]½= 94,12
La quantité économique est de :
7843 / 94,12 = 808,45 soit 8 commandes de 100 tonnes
Le plan annuel d’approvisionnement est donc le suivant :
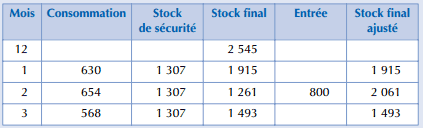
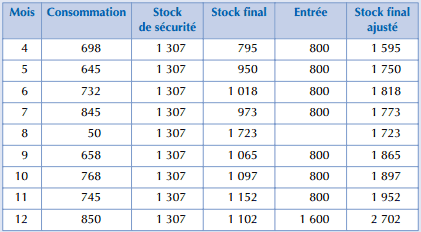Le stock final ajusté ne doit jamais être inférieur au stock de sécurité. Par ailleurs, les commandes sont effectuées sur la base de la quantité économique optimale. Ce mode de gestion de stock combine l’optimisation des flux avec les préoccupations de sécurité d’approvisionnement.
Le budget prévisionnel des achats est, en conséquence, le suivant :
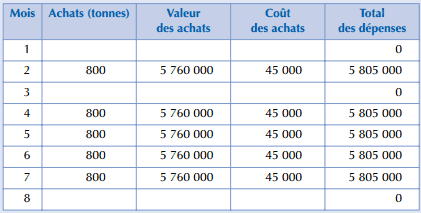
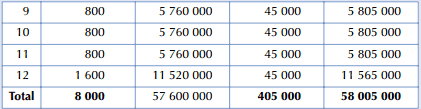Les modèles probabilistes reposent sur des hypothèses simplificatrices, car ils éliminent certains risques majeurs dont la survenue risque de mettre en cause la pérennité de l’entreprise. Si l’on postule que la consommation d’un produit suit une loi normale, le risque de rupture de stock signifie que, pendant le délai de réapprovisionnement, la demande excède le stock de sécurité.
On suppose donc implicitement que la rupture des livraisons n’est pas consécutive à la disparition des sources d’approvisionnement, mais à un simple retard logistique.
Probabilité (rupture d’approvisionnement) > Probabilité (demande > demande moyenne pendant le délai d’approvisionnement + stock de sécurité incompressible)
Application numérique
La consommation est évaluée à 65 unités par semaine en moyenne, avec un écart-type de 45. Si la demande moyenne pendant le délai d’approvisionnement et le stock de sécurité correspondent à 3 semaines de consommation, alors la probabilité de rupture de stock est égale à:
Probabilité ( C > 65 . 3 ) = 1- Probabilité ( t < ou = [((65 . 3) – 65) /45]) = 1 – π(2,89) = 1 – 0,9981 = 0,19 %
Ce résultat est indiqué dans la table de la fonction intégrale de la loi normale. Il convient donc de calculer au préalable la variable centrée réduite [(variable – moyenne) / écart-type]. Si le délai est porté à 1 semaine, ce risque est égal à 50 %. Si ce délai est porté à 2 semaines, ce risque est égal à 7,49 %. Si le délai est porté à 4 semaines, le risque est quasiment inexistant. Cet exemple montre que la probabilité de rupture de stock croît de manière exponentielle avec la politique du « stock zéro ». Un stock de sécurité de 2 semaines permet de contrer efficacement ce risque.
olivier
j’ai un exo et j’aimerais avoir votre aide
Dossier Collectif : Exercice 3 : Gestion de 2 produits séparément puis simultanément
exo 1
Vous êtes responsable de l’approvisionnement de deux produits A et B fournis par un même fournisseur.
Le taux de possession, en raison de la nature des produits s’élève à 50% par an.
Le coût de lancement, y compris, entre autres, le coût du transport est de 1200 € si vous commandez un seul produit et de 2000 € si vous commandez les deux produits simultanément. Le fournisseur propose des remises sur facture
5% si le montant de la facture atteint 200 000 €
7% si le montant de la facture atteint 500 000 €.
La demande pour le produit A est de 2 400 unités par an. (Prix de A : 800 €).
La demande pour le produit B est de 600 unités par an. (Prix de B : 360€).
NB: Les coûts de lancement ne doivent pas être pris en compte dans le montant de la facture.
Questions
1) Étude des produits A et B gérés séparément
Dans un premier temps, vous ne cherchez pas à profiter des rabais offerts et vous résonnerez uniquement sur le produit A
1) Calculez la quantité économique de lancement et le coût total annuel ? Vous cherchez à bénéficier de la réduction de 5%.
2) Calculez la quantité de la commande et le coût annuel total.
3) Quelle conclusion en tirez-vous?
4) Calculez la quantité de la commande
5) Calculez le coût annuel total.
6) Quelle conclusion en tirez-vous?
2) Les produits A et B sont commandés simultanément On pourra commencer par calculer les N* avant les Q* a) Vous ne cherchez pas à profiter des rabais offerts.
1) Calculez le nombre optimal de commandes par an,
2) Calculez la quantité commandée pour A, la quantité commandée pour B
3) Calculez le coût total annuel.
3
b) Vous cherchez à obtenir le rabais de 5%.
1) Calculez le nombre optimal de commandes par an,
2) Calculez la quantité commandée pour A,
3) Calculez la quantité commandée pour B
4) Calculez le coût total annuel.
5) Quelle conclusion tirez vous
Exercice 2 : Demande Fluctuante et rupture
L’entreprise « Auto pièce » prévoit d’obtenir une livraison de pièces au début de chaque trimestre. Chaque livraison doit permettre de faire face aux consommations du trimestre. Le 31 décembre, il reste un stock de 200 unités que l’entreprise envisage de conserver comme stock de sécurité.
Les consommations prévues sont les suivantes :
1er trimestre 4500
2ème trimestre 2700
3ème trimestre 1800
4ème trimestre 3600
Les consommations sont régulières au cours d’un trimestre et le mois comprend 30 jours.
1) Présentez l’évolution du stock sous forme d’un graphique en dents de scie
2) Calculez le niveau du stock d’alerte(le niveau de stock seuil, à partir duquel on doit commander) et présentez le sur le graphique, et cela compte tenu d’un délai d’approvisionnement habituel de 2 mois.
3) Déterminez le nouveau niveau du stock de sécurité que l’entreprise doit posséder pour faire face aux demandes des clients, si au mois de juillet, la consommation se poursuit au même rythme qu’au mois de juin
4) Si la consommation du mois de juillet se poursuit au même rythme qu’au mois de juin (et si l’entreprise n’augmente pas son stock de sécurité), quelle sera le moment et la quantité de rupture de stock(quand le niveau de stock passe en dessous de zéro).