L’intérêt simple est calculé dans le cadre des opérations à court terme (moins d’un an). Par exemple, lorsqu’une banque décompte des intérêts de découvert ou encore lorsqu’une entreprise facture des intérêts de retard à un de ses clients.
Calcul de l’intérêt
L’intérêt est obtenu par application de la formule suivante :
I = Ctn/36 000.
Avec :
– I = montant de l’intérêt,
– C = capital placé ou prêté,
– t = taux d’intérêt annuel,
– n = durée exprimée en jours ou en mois (si la durée est exprimée en mois, le dénominateur est alors 1 200).
Le décompte de la durée en jours est effectué dans le cadre de conventions généralement acceptées pour les opérations financières. C’est-à-dire que la durée est définie en nombre de jours exacts, le premier jour non compris et le dernier jour compris.
◆ Exemple:
Un capital de 5 000 e est placé à intérêts simples au taux annuel de 3 % du 10 février au 15 juin de la même année. La durée sera égale à :
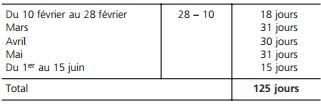
Et l’intérêt sera égal à : I = (5 000 × 3 × 125)/36 000 = 52,08 €.
La valeur acquise par le capital initial
La valeur acquise par un capital est égale au montant du capital augmenté des intérêts acquis. Dans l’exemple ci-dessus, la valeur acquise est donc égale à : 5 000 + 34,72 = 5 034,72 €.
L’intérêt composé est calculé dans le cadre des opérations à moyen ou long terme.
Les modalités de l’intérêt composé
L’intérêt composé est calculé dans le cadre des opérations à moyen et long terme (plus d’un an). Par exemple, à l’occasion d’un emprunt accordé par une banque à une entreprise ou à un particulier.
Le système des intérêts composés se caractérise par la capitalisation des intérêts : les intérêts acquis à la fin d’une période portent intérêts sur les périodes suivantes.
◆ Exemple
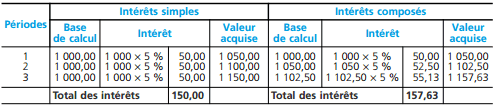
Un capital de 1 000 e est placé pendant 3 ans au taux annuel de 5 % :
Dans le cadre des intérêts composés, la somme que l’on recevra dans 3 ans sera égale au capital initial auquel s’ajoutent les intérêts cumulés, soit : 1 000 + 157,63 = 1 157,63 €.
La valeur acquise à l’issue de n périodes est égale à :
Vn = Vo(1+t)n
Soit : Vn = 1 000(1,05)³= 1 157,63 €.
Avec :
Vn : Valeur acquise, t : Taux d’intérêt, Vo : Capital initial, n : Durée.
L’actualisation
Actualiser, c’est déterminer la valeur aujourd’hui (valeur actuelle) d’une somme que l’on doit recevoir ou payer plus tard.
Pour cela, on utilise la formule suivante :
V0 = Vn(1 + t)–n
Avec :
V0 : Valeur actuelle, t : Taux d’intérêt, Vn : Valeur acquise, n : Durée.
◆ Exemple
On doit recevoir la somme de 6 545 € dans 4 ans.
La valeur actuelle correspondante au taux annuel de 5 % sera égale à : 6 545(1,05)-4 = 5 384,59 €.
Il est donc équivalent, au taux de 5 %, de recevoir 6 545 € dans 4 ans ou 5 384,59 € aujourd’hui.
FABRICE
Très compréhensible. Je profite demander des exercices en informatique sur les algorithmes
David
J’aime vraiment ! Ces cours me donne des précision en mathématique financière ! Je vous encourage de continuer à me les envoyés ! Merci !
Ahmed Babe
Bonsoir j’aimerai savoir la solution de l’excercice
Un individu a le choix entre deux modes de placement : soit un placement A àintérêts simples au taux de 4% l’an, soit un placement B à intérêts simplesprécomptés au taux de 3,9% l’an.a- Lequel de ces deux placements est le plus intéressant ?b- Pour quel taux annuel d’intérêt simple précompté le placement B est-il équivalentau placement A
Kei
j’ai le même exercice à faire et je bloque. Si vous avez trouvé la solution, je ne suis preneuse
Bien-Aimé
Je n’ai pas le temps de lire et de mettre en pratique
une formation
Voici le PRODUIT que je cherche :
j’nvestis 1000 euros à
Intérêts composés
j’ajoute 100 euros chaque mois à mon investissement
Durant 10 ans.
est-ce que vous avez ce produit ?