Une entreprise horticole de la région utilise 10 000 sacs de compost par année (D) dans la confection de pots de plantes et de fleurs et pour satisfaire les commandes et les besoins de ses clients. Chaque sac s’achète au prix de 7$ (Cau). S’appuyant sur des données très récentes, les gestionnaires de l’entreprise estiment que le coût pour passer une commande (Ccu) s’élève à 20 $ et que le coût de stockage se chiffre à 20% du coût unitaire d’un sac de compost, soit 1,40$ (20% * 7$).
On fait l’hypothèse que l’on fonctionne en condition de certitude et, par conséquent, on ne prévoit pas conserver de stock de sécurité (S min = 0).
La personne responsable des achats dans cette entreprise se demande quelle serait la quantité économique à commander QEC pour minimiser le coût total annuel de la gestion des stocks ?
Pour voir le cours ( Cours sur la gestion des stocks)
Solution de l’exercice sur la gestion des stocks
Résumons les données de départ:
Les coûts unitaires:
– Ccu = 20 $ (coût pour passer une commande);
– Cau = 7 $ (coût d’acquisition d’un sac de compost);
– Csu = 1,40$ = (20% x 7 $) (coût de stockage d’un sac de compost).
Les quantités :
– S min = 0 on ne considère aucun stock de sécurité;
– S max = Q + S min = Q
– D = 10 000 sacs consommation durant l’année.
Sans avoir de base en gestion des stocks, la personne responsable des achats pourrait essayer diverses valeurs pour la quantité commandée (Q) et essayer de déterminer visuellement laquelle entraîne le coût total annuel de la gestion des stocks le plus bas, et retenir celle-ci.
Illustration permettant de trouver à tâtons la quantité économique à commander QEC en calculant le coût total annuel de la gestion des stocks en fonction de diverses quantités commandées (Q). Ensuite, on pourra retenir que QEC = Q associé au coût total annuel de la gestion des stocks le plus bas.
En utilisant les formules mathématiques suivantes :
a) pour calculer les coûts de stockage :
Cs = Csu * (S max + S min) / 2 = Csu * (Q / 2)
Les coûts de stockage pour l’année égalent le stock moyen en entrepôt (quantité minimale durant l’année, plus quantité maximale durant l’année, et la somme est divisée par 2 pour avoir une moyenne), multiplié par le coût de stockage d’une unité pendant un an.
Supposons que la quantité commandée Q soit de 200 unités pour chaque commande, alors :
S max = 200 (car il ne peut jamais y avoir plus d’unités que cela à tout
moment de l’année dans l’entrepôt)
S min = 0 (car il n’y a pas de stock de sécurité : condition de certitude)
Csu = 20% du prix d’achat d’un sac, soit 1,40$ comme déjà montré.
Cs = 140$ = 1,40$ * (200 +0)/2
b) pour calculer les coûts de commande pour l’année :
Cc = Ccu * (D / Q)
Le nombre de commandes dans l’année est égal à la demande annuelle (D) divisée par la quantité commandée dans une commande (Q). Les coûts de commande Cc pour l’année sont égaux au nombre de commandes (D/Q) dans l’année multiplié par le coût pour passer une commande (Ccu) :
Cc = 1000$ = 20$ * (10000/200), puisque nous supposons que Q = 200.
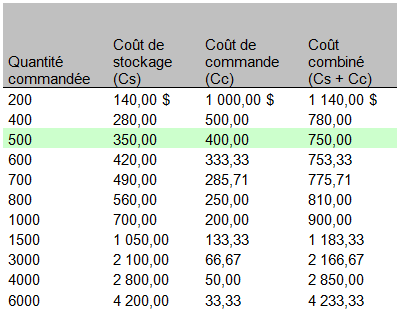
Les résultats que le responsable des achats a obtenus en faisant varier la quantité commande Q, sont résumés dans le tableau suivant :
Remarque :
On ne tient pas compte du coût d’acquisition et du coût de rupture, pour la simple raison que le coût d’acquisition ne fait pas partie du coût de la gestion des stocks et que nous supposons être en condition de certitude (pas d’erreur de prévision donc pas besoin de stock de sécurité).
Le tableau précédent de chiffres est exprimé graphiquement ci-après :
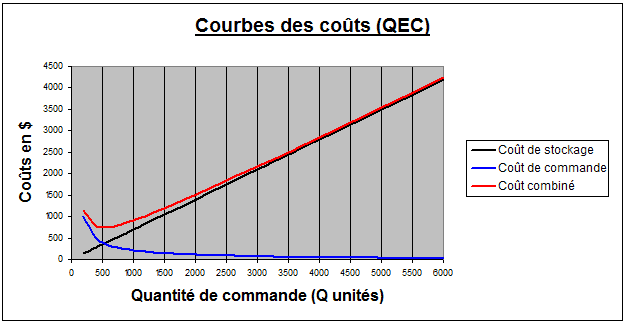 Dans ce graphique, la ligne noire illustre les coûts annuels de stockage. On voit, sur l’axe des Y, que les coûts annuels de stockage augmentent linéairement avec la grosseur de la quantité commandée Q sur l’axe des X. Donc, plus la quantité commandé est grande, plus il y a d’unités en stock et plus les frais de stockage sont élevés.
Dans ce graphique, la ligne noire illustre les coûts annuels de stockage. On voit, sur l’axe des Y, que les coûts annuels de stockage augmentent linéairement avec la grosseur de la quantité commandée Q sur l’axe des X. Donc, plus la quantité commandé est grande, plus il y a d’unités en stock et plus les frais de stockage sont élevés.
La ligne bleue représente les coûts annuels de commande. On voit, sur l’axe des Y, que les coûts annuels de commande diminuent à mesure qu’augmente sur l’axe des X la quantité commandée dans une commande. En effet, plus il y a d’unités dans une commande, moins on fait de commandes dans une année et plus le coût total annuel des commandes diminue.
La ligne rouge représente la somme, sur l’axe des Y, des coûts de stockage et de commande pour l’année en fonction d’une quantité commandée hypothétique sur l’axe des X.
Nous sommes donc intéressés à trouver quelle quantité Q sur l’axe des X est associée avec le point le plus bas sur l’axe des Y de la ligne rouge (coût total annuel de la gestion des stocks).
Comme cela apparaît visuellement, la quantité commandée Q qui minimise le coût total annuel de la gestion des stocks est de l’ordre de 500 unités dans une commande.
Une formule mathématique a été développée par Wilson en utilisant le calcul différentiel pour calculer directement la quantité Q qui minimise le coût total annuel de la gestion des stocks et cette quantité idéale s’appelle QEC (Quantité Économique à Commander).
Il a été établi que le coût combiné le plus bas correspond au croisement de la courbe du coût de stockage et de la courbe du coût de commande. Connaissant cette information, nous pouvons déterminer la QEC d’une façon alternative (algébrique) :
Ccu * D/Q = Csu * Q/2
Soit, après simplification :
QEC = √2(Ccu * D)/Csu
Application de la formule trouvée à notre exemple :
QEC = √2(20$ * 10 000)/(20% * 7$) = 534,522 sacs de compost
Il faudrait donc passer une commande d’une quantité optimale de 534,522 sacs de compost. On remarque que le coût combiné est encore plus précis et plus bas que celui présenté visuellement au graphique précédent.Le fait de ne pas arrondir la quantité commandée permet de vérifier que, au point optimal des coûts de la gestion des stocks, les frais annuels de commande sont égaux aux frais de stockage annuels :
Frais de commande = 374,17 $ = (10000/534,522) * 20$
Frais de stockage = 374,17$ = ((0+534,522)/2) * 1,40$
amn moh
c’est très utile et très simple, je vous remercie, mais j’ai pas bien compris pourquoi on calcule le cout de stock par rapport à la quantité moyenne, et pourquoi on néglige le stock de sécurité ?
lemoudado
On néglige le stock de sécurité car il a été mentionné dans l’énoncé.
Mohamed
je souhaite télécharger aussi le document » Exercice corrigé sur la gestion des stocks » en format pdf
merci